Have you ever wondered about the mysterious point where the perpendicular bisectors of a triangle intersect? Well, that point is called the circumcenter of the triangle. In this article, we will explore the properties of the circumcenter, how to locate and construct it, and solve some examples. So, let’s dive in!
Table of Contents
What is the Circumcenter of a Triangle?
The circumcenter of a triangle is the point where the perpendicular bisectors of all three sides of the triangle intersect. In other words, it is the center of the circumcircle, a circle inscribed inside the triangle. Every triangle has a circumcenter, and it plays a significant role in understanding the geometry of triangles.
The Properties of the Circumcenter
The circumcenter of a triangle has several interesting properties:
Property 1: Equidistant Vertices
The circumcenter is equidistant from all the vertices of the triangle. This means that if you draw lines joining the circumcenter to each vertex, the lengths of those lines will be the same.
Property 2: Isosceles Triangles
When you join the circumcenter to the vertices of the triangle, the resulting triangles are all isosceles triangles. This means that they have two equal sides.
Property 3: Angle Relationships
The angles formed by the circumcenter and the vertices have some interesting relationships. For acute triangles, the angle at the circumcenter, ∠BOC, is twice the angle at vertex A, ∠A. However, for obtuse triangles, the relationship is slightly different: ∠BOC is equal to 2(180° – ∠A).
Property 4: Location of the Circumcenter
The location of the circumcenter depends on the type of triangle:
- Acute Angle Triangle: The circumcenter is located inside the triangle.
- Obtuse Angle Triangle: The circumcenter is located outside the triangle.
- Right Angled Triangle: The circumcenter lies on the hypotenuse of the triangle.
- Equilateral Triangle: In an equilateral triangle, the circumcenter coincides with the incenter, orthocenter, and centroid. It divides the triangle into three equal triangles.
Constructing the Circumcenter of a Triangle
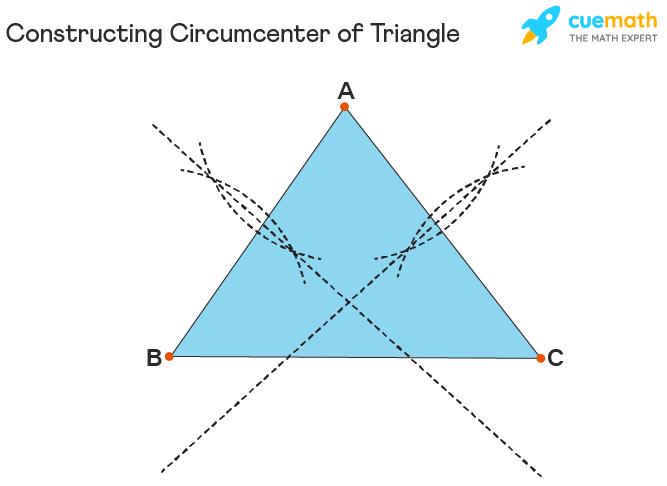
To construct the circumcenter of a triangle, you can use a compass. Here are the steps:
- Draw the perpendicular bisectors of all three sides of the triangle using a compass.
- Extend the perpendicular bisectors until they meet at a point. This point is the circumcenter.
- With the circumcenter as the center, draw a circle passing through any vertex of the triangle. This circle is the circumcircle.
Formulas to Locate the Circumcenter
If you want to locate the circumcenter of a triangle using coordinates, here are some formulas you can use:
Method 1: Using the Midpoint Formula
- Calculate the midpoints of the line segments AB, AC, and BC using the midpoint formula.
- Calculate the slope of any of the line segments AB, AC, and BC.
- Use the midpoint and the slope of the perpendicular line to find the equation of the perpendicular bisector line.
- Find the equation of the other perpendicular bisector line.
- Solve the two perpendicular bisector equations to find the intersection point, which is the circumcenter.
Method 2: Using the Distance Formula
- Find the distances (d₁, d₂, and d₃) between the circumcenter and each vertex of the triangle using the distance formula.
- By comparing the distances (d₁ = d₂ = d₃), you can determine the coordinates of the circumcenter.
Method 3: Using Extended Sin Law
By employing the extended form of the sin law and the distance formula, you can find the radius of the circumcircle and calculate the exact location of the circumcenter.
Method 4: Using the Circumcenter Formula
The circumcenter of a triangle can also be found using a formula that takes into account the angles of the triangle. It relies on the sin of twice the angle and the coordinates of the triangle’s vertices.
Wrap Up
The circumcenter of a triangle is a fascinating point with unique properties. It holds the key to understanding the relationships between the vertices and angles of a triangle. By constructing and locating the circumcenter, we unveil the hidden geometry within triangles. So, the next time you encounter a triangle, don’t forget to ponder the wonders of its circumcenter.
For more information on various topics related to geometry, visit 5 WS.
Related Topics
Explore these related topics to deepen your understanding of triangle properties:
- Incenter
- Orthocenter
- Parts of Circle

